1、地图投影为什么会变形？
要知道变形怎么来，我们就从什么是投影讲起。
(据维基百科)
A map projection is a systematic transformation of the latitudes and longitudes of locations on the surface of a sphere or an ellipsoid into locations on a plane.”
(孙达 蒲英虾 《地图投影》)
所谓地图投影，简单地讲就是在平面上建立与地球曲面上相对应的经纬网的数学法则。
说白了，投影就是将地球表面的坐标网表示在平面上，那么这个用二维展绘三维的方法必定会有许多问题。一个很常举的例子就是把橘子剥皮展开铺在桌子上，那么橘子皮必然会有褶皱或裂隙 ，同样的地球表面展开的话，就一定会产生变形。
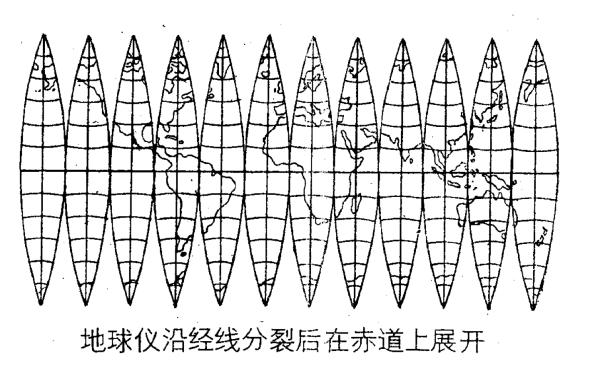
如上图，把地球这个大橘子剥开，沿着赤道拼接，一拉开，就成了一幅地图。
当然，还有别的剥橘子展平的方法，那就是另一种投影了。
变形是研究地图投影的重要部分。
2、地图是怎么投影出来的？
要知道怎么按条件投影，就先要知道投影怎么来。
传统的投影是用光学透视的方法获得的，这样的投影简单易得，但球面与平面的数学关系不容易得到，所以现代地图投影都会采用数学方法进行。
现代地图投影方法分为几何透视法和数学分析法。
传统上的光学透视其实就是在玻璃地球的某个位置放个小灯，灯光在纸上投下的影子就成了一幅地图（也许这就是投影的最初含义了）。比如我把灯放在球心，就得到球心投影。
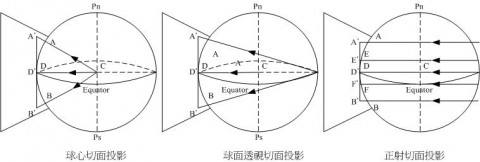
但是这用小灯泡画图的话，只能得到地图，有没有方法可以不用通过灯就能把地图做出来同时又能得到球面与平面的数学关系呢？
后来的地图投影就开始用数学方法来投影了。之前的光学透视的投影我们运用光学原理的知识，应该是能算出平面与球面的数学关系的。
这种关系是怎样的呢？我们将球面投影为平面，那么球上的任意一点P，就肯定能在平面上找到一点P’。那么所谓的地图投影，难道不就是一个坐标变换的过程吗？用数学上的话说，那就是映射啊！如果我们用数字表示出P和P’，那么地图投影f 就变成了一个函数啦！
怎么表示一个点呢？那肯定是用坐标！
3、地图与坐标系
坐标系有很多种啊，比如笛卡尔坐标系，极坐标系。
在地理上，坐标系又是怎样的呢？我们现在有两个面，一个是平面，一个是球面（或椭球面）。
地图上的坐标就是平面坐标，我们一般用数学常用的直角坐标和极坐标就好了，不过要注意哦，地理的坐标系和数学的有点不一样，x轴指向的是北边的，也就是说竖起来的那条轴才是x轴。
在地球上的坐标系又是怎样呢？
我们用一个椭球（我们叫他大地椭球体）来近似代替地球吧，至于这个椭球是怎么来的，大家可以参考一下@凃小图的答案。
在这个椭球面上，我们建立了一个地理坐标系，地理坐标系其实也分成天文经纬度、大地经纬度、地心经纬度。天文经纬度可以用于大地测量中定向控制及校核数据，而在地图投影中用的一般是大地经纬度和地心经纬度。
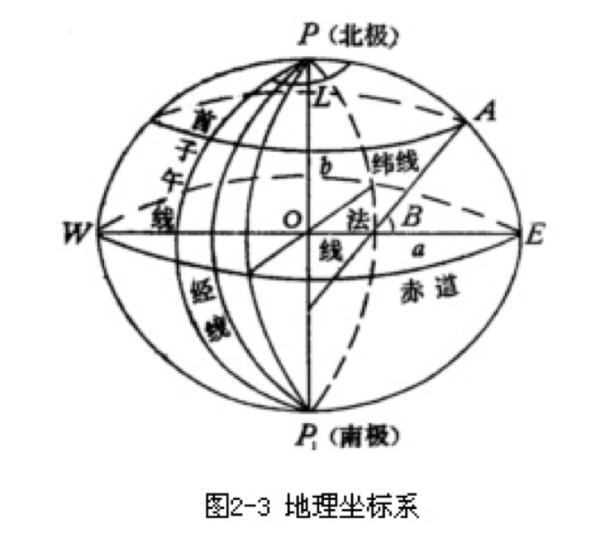
大地坐标系用大地经度和大地纬度来确定面上的点。
大地经度L指过参考椭球面上某一点的大地子午面与本初子午面之间的二面角，
大地纬度B指过参考椭球面上某一点的法线与赤道面的夹角。
地心坐标系的地心指地球椭球体的质量中心。
地心经度等同于大地经度，地心纬度是指参考椭球体面上的任意一点和椭球体中心连线与赤道面之间的夹角。
这经纬度的定义似乎很复杂，嗯，确实很复杂，怎么说的通俗点呢？不如我们不要看这个定义，我们只要知道通过经纬度就能确定这个椭球面上的点就好了。
当然有时候地理研究和小比例尺地图制图对精度要求不高，故常把椭球体当作正球体看待，此时，地理坐标采用地球球面坐标，经纬度均用地心经纬度。
所以我们用数字表示了两个点：
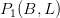或
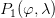表示经纬度。
用直角坐标表示为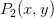
用极坐标表示为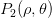
4、再论地图投影
我们知道了地图投影是一个映射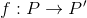
用数字表示P和P’两个点后，就有函数
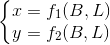好了，我们是可以通过光学透视条件试着求出这个 和 的。以著名的墨卡托为例，（我们略过数学证明）其投影公式是：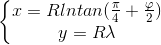
5、地图变形
讲了这么久，终于扯到变形啦。
在保持图形完整性前提下，将（椭）球面转化为平面，投影后得到的经纬线网形状必然会产生变形，也就是说，在投影的过程中，变形是必然存在的。
投影变形使地物的几何特性发生了变化，变形一般包括长度、面积、方向（角度）变形。
为了直观地体验或描述变形，我们造了个变形椭圆，我们在球上画一个小圆圈，这个小圈圈投影到平面上就会变成一个椭圆了，直观地表现了投影变形，看看这些图咯：
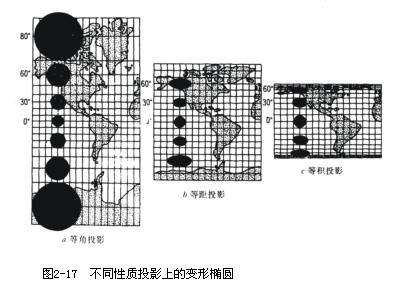但我们要用数字来表示变形啊，这样才能知道具体怎么变形，才能知道是不是等角，不然你看着一个个小圈圈怎么知道它有没有变形啊。
用来描述变形的有长度比、面积比、角度变形。
长度比用来描述长度变形，一个微分线段ds，投影在平面上变成了ds’,那么长度比其实就是ds’与ds的比：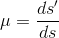
不过呢，这个表示出来的并不是变形，表示变形的话，应该用变形的长度比上原长度。
所以我们这样表示长度变形：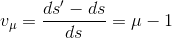
然而这还不够，不同方向的线段变形不一样啊，我们一般只看四个方向的长度比。过同一个点的线段，有的方向的变形大，有的方向变形小，变形最大的叫极大长度比a，最小的就叫极小长度比b，这两个方向其实就是变形椭圆的长半径和短半径方向。我们称这两个方向为主方向。有时候主方向就是经纬度方向（m，n），当然有时候不是。
面积比P就是变形前后的面积比，很容易就可以知道，P=ab。
角度变形则是指投影前后角度的差值
其中β 指一个方向与主方向的夹角，当差值最大时（记为ω/2）有：
ω称为最大角度变形
利用数学方法，我们可以通过a和b来考察某个投影的变形。此处就不细讲了。
6、怎么控制地图变形。
对于一些几何投影，比如方位投影、圆柱投影等，他们是有自己的投影公式的。
比如利用已知条件和光学透视我们可以知道正轴圆柱投影都满足以下通式。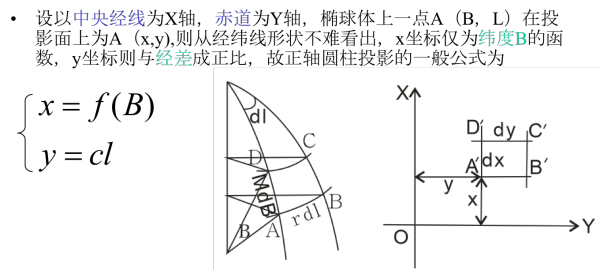
其变形也有公式，推导如下：
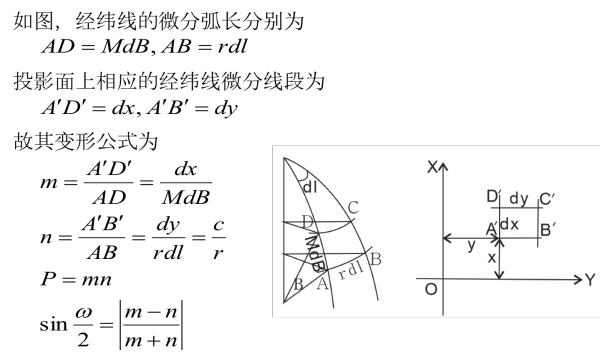这样，如果我们限定变形条件比如使得m=n（等角条件），把mn代入就有一条方程了，积分一下就可以算得投影公式。
这里等角条件m=n；等积条件P=mn=1
至于等距条件，就是是对应长度比为1（实际上是任意投影的一种）
到后来的伪投影、派生投影也都是通过量化变形来得到投影公式从而达到控制变形。
总结
1、地图开始是通过光学透视投射出来的，这就是投影的由来
2、后来人们开始通过数学计算变换坐标系的方式来进行抽象的投影，不再是拿着小灯泡照来照去了。
3、地图投影必定会产生变形，我们用长度比、面积比和角度变形来表示这些变形，从而分析投影变形。
4、反过来如果我们要控制变形得到按条件的投影，我们就用对应的变形条件，通过数学推导到处对应的变换公式。
2017.03.31 下午 于珠海
问题原载于知乎 - 地图投影怎么做到按条件（等角、等面积、等距）投影的？ - 罗皓文的回答