0. 前言
上一次写blog居然已经是4个月之前了，这学期课虽不多，但各种零零散散的事情总是在忙，再加上上半学期几乎天天都要早起，也不知道为什么我还天天都晚睡，然后就很累。
这周是期中考假期，一周下来好像没干啥，值得纪念的就是天天在外面各种地方吃了许多奇奇怪怪的好吃的，嗯，真难得有机会出去玩。昨天在机房值班，天气颇好，卡了很久的作业又有了做下去的方向，心情十分舒畅，于是花了一个多小时造了个轮子（写了一个梯度下降）。稍微整理一下，写一篇blog当作笔记吧。
讲真，到现在为止我也没有自己实现过梯度下降的算法，于是我很兴奋地就开始干了。
梯度下降原理很简单，我也不知道为什么各种书讲得很不清楚（其实是太多细节导致乍一看抓不住主干）。
梯度下降和最小二乘法有点像，梯度下降可以用来求解最小二乘法问题，但除此之外，还能求解其他得优化问题。
可以说，只要是函数，都能用梯度下降来求最小值，不过求到得也只能是局部最小值。
1. 机器学习的套路
不管你听哪个老师的课，看哪一本机器学习的书，一开始讲有监督学习时基本上是这个三步走套路，我称之为HLO——Hypothesis，Loss，Optimization。
首先要明确有监督学习要解决的问题：给定特征x，求一个y。这个y可以是连续的、也可以是离散的，y连续时就是回归问题，y离散时就是分类问题。如果我给了你很多x和对应的y，下次我给你新的x你能不能算出对应的y呢？
[1] Hypothesis
对于一个n维向量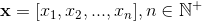
定义函数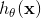
该函数称为Hypothesis，我们假设通过该函数可以算出预测值。值得一提的是，这里的m维向量
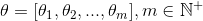是参数，θ只要确定了，函数就能确定，但因为有很多个θ，所以Hypothesis可以看成是一个函数集合，我们要做的就是从所有θ的组合中找出最优秀的θ，确定h(x)。
[2] Loss
算出的预测值和真实值y还是有区别的，所以我们定义了一个Loss函数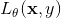
以量化这种区别，一般来说我们会使得Loss随着预测值接近真实值y而变小。
[3] Optimization
对于同样的x，不同的θ算出不同的预测值，因此Loss也会不同，所谓“最优秀的”θ，就是使得Loss最小的θ嘛！那么，我们实际上就是求Loss的最值问题，也就是优化问题（Optimization）。
2. Least Square
说起Gradient Descent就会让人想起Least Square。
我们看看Loss函数，简单粗暴地算预测值和真实值y的差，取平方去掉正负号，故有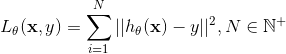
这里N是所有训练样本，这个函数越小，预测值自然越接近真实值y。
最值处的必要条件就是导数为零（最值点必为极值点），于是，简单粗暴地求偏导并使之为零。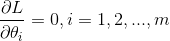
解这个方程，解的θ就是极值点。对于L为凸函数的问题，该方程只有一个解，非凸的话自然有多个解，如果能求到多个解自然可以比较多个解里面那个θ更优秀啦，可是很难把所有解都找出来。
凸函数问题的话，最典型的就是线性回归了，一般我们第一次接触最小二乘都是在学线性回归的时候，也就是定义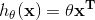
考虑bias的话
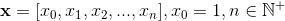然后求Loss的的偏导数，直接解方程，可以得到具体得公式，这种可以将解用通式表示的解的形式叫closed-form。不是closed-form的可以用迭代法来求解，迭代法常用的有Newton’s Method，还有就是我们这里的Gradient Descent了。
小结一下：
最小二乘的本质就是定义了一个Loss函数。
梯度下降是求解最小二乘的一种算法。
3. Gradient Descent
然后我们就开始讲Gradient Descent了。
我们可以暂时忘记最小二乘了，要把握住算法，最重要地是丢掉细枝末节，我们这里地Loss是可以任意定义地，它就是一个函数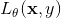
我们的问题仍旧是：找一个θ使得Loss最小。
梯度下降的做法是：
- 先随便瞎猜一个θ;
- 然后把Loss看成θ的函数,计算Loss的梯度∇L，根据梯度更新θ;
- 不断重复第2步使得Loss基本不变.
更新梯度的公式为
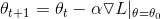
这里的α是学习率，简单理解就是参数更新的步长，从初始的θ开始移动改变θ，算出的梯度∇L是运动的方向，而α则是我们移动的步长了。常见的说法就是，在山地里面我们不断寻找最陡峭的地方往下走，这样总会找到一个局部最低点。
有一个无聊的人（误）录了一个视频 李宏毅 - ML Lecture 3-2: Gradient Descent (Demo by AOE)，讲世纪帝国里是怎么做的Gradient Descent的。
4. 计算梯度
以上提到的最难的步骤就是计算梯度∇L了，实际上就是分别对各个θ求偏导数而已
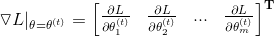
这里的t是指当前已经迭代的次数，而我们知道求偏导数实际就是求一元倒数，所谓导数就是：
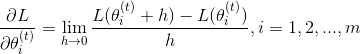
我们将h设成一个很小很小的数，直接代入就能求到近似解了，求到梯度之后就是不断重复迭代就行了。
5. Python实现
首先定义Hypothesis Function和Loss Function：
import numpy as np
# define hypothesis function
def hypothesis(P, X):
# define you hypothesis function here...
return 0
# define loss function
def loss(P, X, Y):
# define you loss function here...
return 0
Hypothesis就是我们的机器学习模型，定义成参数和特征（自变量）的函数，基于Hypothesis定义合适的Loss，一般来说Loss的输入包括了Hypothesis的输入，同时还需要输入实际值/Ground True（因变量）。
这里没有定义具体的Hypothesis和Loss，因为我们主要目的是实现梯度下降的算法。
再次明确我们的目的：优化Loss，求使得Loss为局部最小值时的θ。
首先,定义计算梯度的函数，该函数的输入和Loss一样，这里的是依次对各个求导，注意自变量是P，输入X、Y一般是训练样本。直接用导数的定义公式，把dh设成1e-7(足够小的值)。
# count gradient
def gradient(P, X, Y):
nP = len(P)
D = np.zeros(nP)
for _i in range(nP):
dh = 1e-7
h = np.zeros(nP)
h[_i] = dh
D[_i] = (loss(P + h, X, Y) - loss(P, X, Y)) / dh
return D
然后定义每一次迭代更新参数的方法，也就是输入当前参数，返回下一参数。每一次计算就是参数减去学习率乘以梯度。最后整个BGD的实现就是循环多次这一步而已。这里lr就是学习率，init_P是初始的参数，X、Y是训练样本，niter是迭代次数，这里每迭代一定次数（vbose）打印一下当前的Loss。
# BGD Algorithm
def BGD(lr, niter, init_P, X, Y, vbose=1000):
P = init_P
for _i in range(niter):
P -= lr * gradient(P, X, Y)
if (_i % vbose == 0):
print("iter:%s, loss: %s" % (_i, loss(P, X, Y)))
return P
6. 例子
为了测试我们的算法，我写了两个例子，试运行了一下。
1. 多元线性回归
定义多元线性回归的函数，h(X)=PX。基于最小二乘原理定义损失函数。
def hypothesis(P, X):
# h(X) = PX
bias = np.ones(X.shape[:-1])
input_ = np.insert(X, -1, bias, axis=-1) # channel_last
return np.dot(input_, P)
def loss(P, X, Y):
# Square Loss
d = (Y - hypothesis(P, X)) ** 2
return np.sum(d) / len(d)
生成一些随机样本，这里设置3个自变量，因此有4个参数（还有一个常数项），生成2000个随机的X并求出对应Y。这里还加了一点噪声。
X = np.random.rand(2000, 3) # random samples
para_t = np.array([115, -12, -3, 44],dtype=np.float64) # true_parameters
Y = hypothesis(para_t, X) + np.random.rand(1)
print(X)
print(Y)
因为是凸优化，所以是唯一解，不用考虑局部最优，所有随意初始化都能求到结果啦。那我们初始化参数设为0，开始训练，然后把参数打印一下。
para = np.array([0, 0, 0, 0],dtype=np.float64) # init_para
print("Para_h: %s" % BGD(0.01, 10000, para, X, Y))
print("Para_t: %s" % para_t)
结果如下：
iter:0, loss: 6051.55206953
iter:1000, loss: 51.0304688772
iter:2000, loss: 5.0273756556
iter:3000, loss: 0.68016847629
iter:4000, loss: 0.101467038909
iter:5000, loss: 0.0154896290322
iter:6000, loss: 0.00237660362235
iter:7000, loss: 0.000365047416709
iter:8000, loss: 5.60845545895e-05
iter:9000, loss: 8.61695483353e-06
Para_h: [ 114.99777458 -12.0023768 -2.05467269 43.99780741]
Para_t: [ 115. -12. -3. 44.]
Para_h是我们拟合出来的参数，Para_t是真实的参数（基于这个函数生成模拟样本的），解这个就是a peace of cake啦。
2. 简单的人工神经网络
数据是Nerlove收集的1955年145家美国电力企业的总成本(TC)、产量(Q)、工资率(PL)、燃料价格(PF)及资本租赁价格(PK)，X为(Q, PL, PF, PK)，Y为TC。
别听神经网络好像很腻害的样子，本质就是花式堆叠广义线性回归。还是先定义Hypothesis和Loss，这里定义了一个reLU函数作为激活函数，Hypothesis是一个只有两个隐含层的神经网络，输入层有4个神经元，第一层有6个神经元，第二层有3个神经元，一共有47个参数。
reLU定义如下：
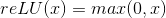
def reLU(X):
return X * (X > 0)
def hypothesis(P, X):
# ANN(2 Layers)
p1 = P[:5]
p2 = P[5:10]
p3 = P[10:]
bias = np.ones(X.shape[:-1])
input_ = np.insert(X, -1, bias, axis=-1) # channel_last
nn11 = reLU(np.dot(input_, p1))
nn12 = reLU(np.dot(input_, p2))
nn1 = np.stack([nn11, nn12, bias], axis=-1)
return reLU(np.dot(nn1, p3))
def loss(P, X, Y):
# Square Loss
d = (Y - hypothesis(P, X)) ** 2
return np.sum(d) / len(d)
# Load Data
data = np.loadtxt(r'data.csv', delimiter=',')
Y = data[:, 0]
X = data[:, 1:]
X.shape # (145L, 4L)
# get train sample and test sample
N = 100
Ytrain = Y[:N]
Xtrain = X[:N, :]
Ytest = Y[N:]
Xtest = X[N:, :]
一共145个样本，我们用100个做训练，45个做测试，先跑一下。
para = np.random.rand(47)
print(para)
print(BGD(1e-3, 5000, para, Xtrain, Ytrain, 1000))
print("RMSE:%s" % loss(para, Xtest, Ytest) ** 0.5)
结果如下：
iter:0, loss: 32.43822935
iter:1000, loss: 32.43822935
iter:2000, loss: 32.43822935
iter:3000, loss: 32.43822935
iter:4000, loss: 32.43822935
RMSE:41.5248204328
发现结果坏掉了，打印一下预测值，发现全部变成0了，再打印一下梯度。发现梯度全是0，这就是传说中的Gradient Vanish，在神经网络多层传播后，参数的变动很有可能无法计算出梯度（梯度弥散，Gradient Vanish），又或者参数的微微变动就会导致梯度骤变（梯度爆炸，Gradient Explosion）。
Y_hat, Y, dY
[[ -0. 11.982 11.982]
[ -0. 16.674 16.674]
[ -0. 12.62 12.62 ]
[ -0. 12.905 12.905]
...]
...
[ 0. 0. ... 0. 0.]
事实上我们这里算出来的梯度也是很大的，因此把学习率调成了一个很小的值（1e-7），再多跑几次（使得初始化参数落到了一个比较好的位置上）。出来的结果还是能看的。
iter:0, loss: 56115.2138837
iter:1000, loss: 2.58377124655
iter:2000, loss: 2.20030671483
iter:3000, loss: 1.88540868509
iter:4000, loss: 1.6693258371
RMSE:10.2699172204
...
Y_hat, Y, dY
[[ 12.94779536 11.982 -0.96579536]
[ 13.91592103 16.674 2.75807897]
[ 14.50662844 12.62 -1.88662844]
[ 13.98164501 12.905 -1.07664501]
...]
...
[ 186.86534503 -4.51131314 ... 2328.47006998 4.02859825]
7. 总结
大概写了一下BGD的笔记，还是有一点收获的，也算是加深了对梯度下降理解啦。
不过不知道为什么，代码只写了不到一个小时，写blog却写了一天（心累）。
代码已上传到Github - MLD01_BGD。
2018.05.13 晚上 于广州